投影变换基本概念
地图投影的概念
地图投影的基本问题是如何将地球表面(椭球面或圆球面)表示在地图平面上。由于地球椭球面或圆球面是不可展开的曲面,即不可能展开成平面。而地图又必须是一个平面,所以将地球表面展开成地图平面必然产生裂隙或褶皱。在编制地图中,要求(在地图上)得到连续的经纬网格,有裂隙或重叠的经纬网格不符合编图要求。如果采用简单的方法将有裂隙或重叠的经纬网“拉伸”或“压缩”使之连续,也不能符合编制地图的实际需要,因此,编制地图必须采用地图投影的方法,将地球表面的经纬网格用各种方法投影到地图平面上,才能满足多种编图要求的各种连续的经纬网格。
地图投影即为地球椭球表面(或地球球体表面)与地图平面之间点与点(或线与线)相对应。如设地球表面上某一点的地理坐标为(Q、λ),其地图平面上相应点的直角坐标为(x,y),则表示地球表面经线和纬线的两族平面曲线的方程为:
Q = F1(x,y) λ= F2(x,y)
对x和y分别得出的:x = f1(Q,λ) y = f2(Q,λ)
当函数f1和f2在表象区域内连续和单值时,上述方程表示曲面上坐标为(Q,λ)的一点在平面上只有一个点与之对应,我们把这个方程视为地图投影的一般方程。可以说,地图投影就是建立地球表面上点(Q,λ)和平面上的点(x,y)之间的函数关系式。地图投影学就是研究地球表面上的点或线表示在地图平面上的理论与方法。
地图投影的要素
大地测量中用水准测量方法得到的地面上各点的高程是依据一个理想的水准面来确定的,这个水准面称为大地水准面。大地水准面所包围的球体称为大地球体。以一个大小和形状同它极为接近的旋转椭球面来代替,以椭圆的短轴(地轴)为轴旋转而成的椭球面称为地球椭球面。椭球体的元素与公式如下:
扁率:af=(a-b)/a
第一偏心率:e2=(a2-b2)/a2
第二偏心率: ep2=(a2-b2)/b2
其中:长半径a(赤道半径),短半径b(极轴半径),扁率af,第一偏心率e,第二偏心率ep。
下面介绍地球椭球体表面上的基本点、线、面和地理坐标系的概念。
垂直于地轴,并通过地心的平面叫赤道平面。赤道平面与地球表面相交的大圆圈(交线)叫赤道,平行于赤道的各个圆圈叫纬圈(或纬线),显然赤道是最大的一个平行圈,它的半径为a。通过地球表面垂直于赤道面的平面叫经面或子午面,它和地球表面相交的线叫经线圈(经线)或子午圈,所有的子午圈长度彼此都相等,均为一长半径等于a,短半径等于b的椭圆。由地球椭球体上的任一点可以引一垂线垂直于该点的地平线(切线),这条垂线称为法线,这条线与赤道面相交所构成的角叫地理纬度(简称纬度),通常用希腊字母Q表示,纬度以赤道为0°,向北、南两极各以90°计算,向北叫北纬,向南叫南纬。
通过地球表面上某一点的经线面与起始经线面的夹角叫做地理经度(简称经度),通常以希腊字母λ表示。地面上任一点的位置,在测绘工作中通常是用经度(λ)和纬度(Q)来决定,写成M(φ,λ),经线和纬线是地球表面上两组正交(相交为90°)的曲线,这两组正交的曲线构成的坐标称为地理坐标系。地表面某两点经度值之差称为经差,某两点纬度值之差称为纬差,如若两点在同一经线上,其经差为零,如在同一纬线上,其纬差为零。
MapGIS 10提供了116种椭球体参数数据,全部封装在系统中,下面列出了几个常见的椭球体参数:
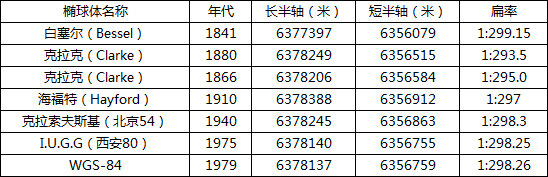
还支持自定义的椭球体参数编辑。方法是找到安装程序program目录下的ellip.dat文件,用记事本打开,找到第6行按照上面的格式编辑数据,就可以在程序里使用该椭球体参数。
我国常用的大地坐标系及不同坐标系转换
采用不同的椭球,就会得到不同的坐标系,因此椭球参数的更新也叫大地坐标系变换。当前我国采用的主要坐标系有:
(1)1954年北京坐标系
该坐标系是通过与原苏联1942年坐标系联测而建立的。解放后,为了建立我国天文大地网,鉴于当时历史条件,在东北黑龙江边境上同苏联大地网联测,推算出其坐标作为我国天文大地网的起算数据;随后,通过锁网的大地坐标计算,推算出北京点的坐标,并定名为1954年北京坐标系。因此,1954年北京坐标系是苏联1942年坐标系的延伸,其原点不在北京,而在苏联普尔科沃。该坐标系采用克拉索夫斯基椭球作为参考椭球,高程系统采用正常高,以1956年黄海平均海水面为基准。
(2)1980年西安坐标系
1978年4月召开的“全国天文大地网平差会议”上决定建立我国新的坐标系,称为1980年国家大地坐标系。其大地原点设在西安西北的永乐镇,简称西安原点。椭球参数选用1975年国际大地测量与地球物理联合会第16界大会的推荐值。简称IUUG-75地球椭球参数或IAG-75地球椭球。
(3)新1954年北京坐标系
将全国大地网整体平差的结果整体换算到克拉索夫斯基椭球体上,形成一个新的坐标系,称为新1954年北京坐标系。该坐标系与1980年国家大地坐标系的轴定向基准相同,网的点位精度相同。
(4)WGS84坐标系
在GPS定位中,定位结果属于WGS-84坐标系。该坐标系是使用了更高精度的VLBL、SLR等成果而建立的。坐标系原点位于地球质心,Z轴指向BIH1984.0协议地极(CTP)。
(5)不同椭球参数更新
①将原椭球参数下的投影数据资料输入到计算机中变成要素类或者简单要素类。
②将它们添加到地图文档里,并加载投影转换插件,设置好投影参数及源椭球参数和新椭球参数值。
③选择相应的转换功能,系统即自动进行转换,将原椭球参数下的数据转为新椭球参数下的数据。
④浏览转换后的生成的新的要素类或者简单要素类,若正确,则保存下来,即完成了两种不同椭球参数下的数据转换。
MapGIS提供的主要投影变换类型
(1) 通用横向墨卡托投影(UTM)
通用横向墨卡托投影是横轴等角割圆柱投影,圆柱割地球于两条等高圈。该投影将地球划分为60个投影带,每带经差为6度,已被许多国家作为地形图的数学基础。一般从南纬度80到北纬度84度的范围内使用该投影,对于两极地区则采用UPS投影(通用球面极投影)。
(2)亚尔伯斯等积圆锥投影
亚尔伯斯等积圆锥投影即为双标准纬线投影,也即正轴等面积割圆锥投影。该投影经纬网的经线为辐射直线,纬线为同心圆圆弧。亚尔伯斯等积圆锥投影的应用在编制一些行政区划图,人口地图,地势图等方面应用较广。如中国地势图,即是以Q1=25度,Q2=45度的亚尔伯斯等积圆锥投影。
(3)兰伯特等角圆锥投影
兰伯特等角圆锥投影也称兰勃脱正形圆锥投影,该投影的微分圆投影后仍为圆形。经线为辐射直线,纬线为同心圆圆弧。指定两条标准纬度线Q1,Q2,在这两条纬度线上没有长度变形,即M=N=1。此种投影也叫等角割圆锥投影,可用来编制中、小比例尺地图。等角圆锥投影有广泛的应用,特别适宜于作为中纬度处沿纬度线伸展的制图区域之投影,投影后经线为辐射直线,纬度线为同心圆圆弧。我国的分省图,即为两条标准纬度线为Q1=25度,Q2=45度的兰伯特等角圆锥投影。1962年以后,百万分之一地图采用了等角圆锥投影(南纬度80度,北纬度84度),极区附近,采用等角方位投影(极球面投影)。
地图分幅为:
纬度60以下,纬度差4,经差6度分幅;
纬度60-76,纬度差4,经差12度分幅;
纬度76-84,纬度差4,经差24度分幅;
纬度84-88,纬度差4,经差36度分幅;
88-90仍为一幅图。
每幅图内两条标准纬线的纬度:
Q1=QS+40分(南纬度) Q2=QN-40分(北纬度)
投影后经线是辐射直线,东西图幅可完全拼接,南北图幅有裂隙。
我国采用等角割圆锥,Q1=PHIS+35分Q2=PHIN-35分
(4)墨卡托投影(等角正圆柱投影)
等角正圆柱投影也称墨卡托投影,经纬线投影为互相正交的平行直线。该投影在航海、航空应用很广。航海图上的等角航线常使用该投影。使用该投影,等角航线在地图上是一条直线。值得注意的是,等角航线是球面上两点间对所有经线保持等方位角的特殊曲线,不是两点间的最近路线,是一条以极点为渐近点的螺旋曲线。
(5)高斯-克吕格(GAUSS-KRUGER)
高斯-克吕格(GAUSS-KRUGER)是等角横切椭圆柱投影。该投影以中央经线和赤道投影后为坐标轴,中央经线长度比=1。为了控制变形,本投影采用分带的办法。如果将地球划分为60个投影带,每带经差为6度,就是6度分带法;如果将地球划分为120个投影带,每带经差为3度,就是3度分带法。该投影已被许多国家作为地形图的数学基础,一般从南纬度80到北纬度84度的范围内使用该投影。
对于两极地区则采用UPS投影(通用球面极投影)。高斯-克吕格投影通常投影带为6度或3度,超过了6度后变形会增大。一般常用来制作大比例尺的地图投影,如1/50万、1/10万、1/5万、1/1万等。
有关高斯-克吕格3度带和6度带的投影区带号、中央经度、经度范围参见“附录II”。
(6)普通多圆锥投影
普通多圆锥投影的经线为对称于中央经线和赤道的曲线,纬线投影为同轴圆圆弧,弧心位于中央直径线上,中央经线是直线,M=1,纬线与中央经线正交,N=1。该投影适用于沿中央经线延伸的区域(15度范围内)。常用于编制中、小比例尺的数学基础。该投影在美国被广泛应用,是百万分一地图投影的基础。
(7)正轴等距离割圆锥投影
正轴等距离割圆锥投影即双标准纬线投影。等距离圆锥投影在我国应用很少。
(8)横轴墨卡托投影(横切圆柱等角投影)
该投影是把地球看作半径=R的球,如果把地球看作椭球即为通用横轴墨卡托投影或高斯-克吕格投影。该投影等高圈和垂直圈互相正交,经纬线为曲线。墨卡托投影因其经线为平行直线,便于显示时区划分,如时区图、航空图、航海图等。
(9)等角方位投影(或球面投影)
透视投影时,视点在球面上的投影即为等角方位投影。等角方位投影的等角性质和圆投影后仍为圆,常用来作大比例地图的数学基础,其投影格网在工程和科研方面有应用。
正轴投影时,纬线投影后成为同心圆,经线投影后成为交于一点的直线束,两经线间的夹角与实地经度差相等。对于横轴或斜轴的方位投影,则为等高圈和垂直圈,相当于经纬线的线圈。球面投影时,地面上无论大圆或小圆,在投影中的表象仍为一个圆。
(10)等积方位投影
等积方位投影在小比例尺制图中,特别是东西半球图应用很多。如东半球取Q0=0,λ0=70E,西半球取Q0=0,λ0=110W的横轴等面积方位投影。对于水陆半球图常取:Q0=(±)45度,λ0=0或180的斜轴等面积方位投影。
各大洲图常采用斜轴等面积方位投影,中心为:
亚洲图:Q0=+40, LON0=90E
欧洲图:Q0=+52.30, LON0=20E
非洲图:Q0=+0, LON0=20E
北美洲图: Q0=+45, LON0=100W
南美洲图: Q0=-20, LON0=60W
(11)等距离方位投影(波斯托投影)
等距离方位投影从定点或原点(Q0,LON0)向任何地方的方位角与距离都相等。正轴投影用于南北极半球图,横轴投影用于东西半球图,斜轴在实践中也有应用。航空中心站、观测站等常需要这种投影。
(12)心射切面投影(或球心投影)
透视投影时,视点在球心上的方位投影为心射切面投影。使用该投影,地球上的任何大圆面如经线圈投影后成为直线。
正轴时,经线为交于原点的辐射直线,纬线为同心圆。
横轴时,经线为平行直线,离中央经线愈远,间隔越大。
(13)正射方位投影
透视投影时,视点在无穷远处的方位投影为正射方位投影。使用该投影,经纬线投影后一般为椭圆。正射投影很少用来编制地图,常用来编制星球图。从地球看星球可以看作是正射投影。
(14)垂直近距离方位投影(或外心投影)
透视投影时,视点在球面外的方位投影为外心投影。具体应用时,距离越大,投影范围也越大。外心投影在制作富有立体感的宣传图中应用较多。在研究空间像片的数学模式中得到应用。
(15)正弦曲线等面积伪圆柱投影
使用投影后,纬线互相平行,经线对称于中央经线(直线),其余经线为正弦曲线,因此,该投影常称为正弦投影。该投影适用于沿赤道或沿中央经线伸展的地区。
(16)等矩形圆柱投影
等矩形圆柱投影是等距离切圆柱投影(或方格投影)。投影后,经纬线互相平行,且组成相等的方格。该投影适用于沿赤道或沿中央经线伸展的地区。
(17)米勒圆柱投影
米勒圆柱投影是正轴等角切圆柱投影。相当于墨卡托投影,经纬线网为平行直线。
(18)范.德.格林顿投影
该投影为球面投影。1963年设计了等差分纬线多圆锥新投影,取代原来的格林顿投影,弥补了南北极高纬度地区投影误差过大的缺陷等等。
(19)斜轴墨卡托投影
斜轴墨卡托投影为斜轴等角圆柱投影,投影后,等高圈和垂直圈互相正交,经纬线为曲线。
(20)两极球极平面投影
两极球极平面投影是正轴等角方位投影,相当于极点切球面投影。两极球极平面投影一般用于地球两极附近的投影。纬度范围在北纬度84-90,南纬度(-80)--(-90)的投影常用该投影。该投影的纬线投影后成为同心圆,经线投影后成为交于一点的直线束,两经线间的夹角与实地经度差相等。
(21)正切差分纬线多圆锥投影
差分纬线多圆锥投影的一种数学模型。现行的中文世界地图不仅不符合读者“左西右东”的阅读常识,而且由于世界的西时区和东时区被不对称地分割,国际日期变更线既不是中央经线,也不是左右边经线,致使读者难以直观感受时间和日期的变更。为此,中国科学院测量与地球物理研究所高级工程师郝晓光博士提出了一项“以零经度为中央经线的新版中文世界地图”的科学发明。依据这一发明,新版地图以0度经线为中央经线,以西经180度为左边经线,东经180度为右边经线,以正切差分纬线多圆锥投影为数学方案制作。其最大特点是完全符合“左西右东”的阅图习惯和常识。
(22)等差分纬线多圆锥投影
我国地图工作者于1963年创制,是我国编制“世界地图”常用的一种投影。现行世界地图与新版世界地图均采用“等差分纬线多圆锥投影”,这种投影方式的特点是中间变形较小,两侧变形较大。在现行世界地图上,世界陆地基本位于图两侧,变形较大;但中国位于图中偏左,变形较小;在新版世界地图上,中国位于图右侧,变形较大;但世界陆地基本位于图中,变形较小。中国图形在新版世界地图上的姿态非常优美,极富动感。中国的图形面积在新版世界地图上比在现行世界地图上增大了3.1%。
此种投影方式是中国特有的对世界地图的投影方式。因此对于该投影,部分的参数为固定值:如中央子午线经度:必须设置为1500000;水平比例尺单位为“厘米”,比例尺为10000000,否则投影失败。
(23)彭纳投影
彭纳投影即等积伪圆锥投影。为法国人彭纳所创。中央经线是直线,其他经线为对称于中央经线的曲线。纬线为同心圆弧。中央经线和标准纬线上没有变形,离开这两条线越远变形越大。图上所有纬线都保持长度不变,面积相等。彭纳投影常用作大洲图。
(24) Web墨卡托投影
Google Maps、Virtual Earth等网络地理所使用的地图投影,常被称作Web Mercator或Spherical Mercator,它与常规墨卡托投影的主要区别就是把地球模拟为球体而非椭球体。
墨卡托(Mercator)投影,又名”等角正轴圆柱投影“,荷兰地图学家墨卡托(Mercator)在1569年拟定,假设地球被围在一个中空的圆柱里,其赤道与圆柱相接触,然后再假想地球中心有一盏灯,把球面上的图形投影到圆柱体上,再把圆柱体展开,这就是一幅标准纬线为零度(即赤道)的”墨卡托投影“绘制出的世界地图。
几个常见地图投影及其变形
地图表面是个不可展面,当它展开为平面时必然产生破裂或褶皱。“地图投影”就是要解决球面与平面不可展的矛盾。地图投影是按照一定的数学法则,将地球椭球面(或球面)上的经纬线转绘到平面上的方法。它的实质是将地球表面的地理坐标变换为平面坐标,建立两者的函数关系。然后,根据函数关系式计算的数据,在平面上展绘经纬线网。在依据经纬线网所提供的地理坐标将地面上的点一一转绘到平面上去,进而画出由点、线、面符号表示的各种地形地物,从而完成地图的编绘。地图投影是保证地图精确度的重要的数学基础之一。
地图投影的变形可分为长度变形、面积变形、角度变形和形状变形。每一幅地图都有不同程度的变形。在同一幅地图上,不同地区的变形情况也不相同。地图表示的范围越大,变形越大。因此,大范围的小比例尺地图只能供了解地表现象的分布概况使用,而不能用于精确的量测和计算。
几个常用地图投影如下表:
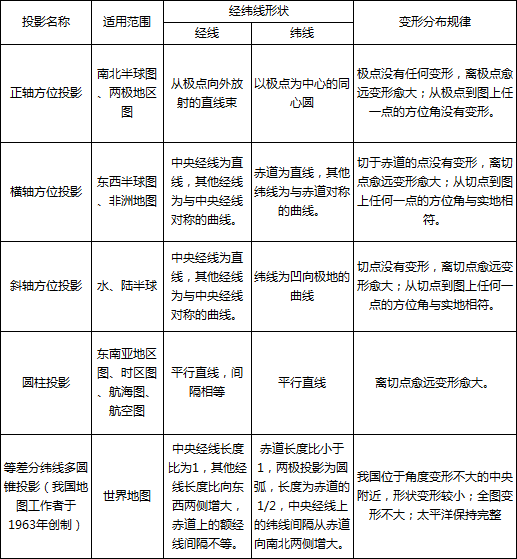
1、根据变形性质的投影分类
①等角投影--地球表面上无穷小图形投影后仍保持相似或两微分线段所组成的角度,在投影后仍保持不变,称等角投影,又称正形投影。在等角投影中变形椭圆为不同大小的圆,它满足条件,极值长度比a=b或经纬线夹角θ=90°和沿经纬度长度比相等(m=n)。
②等面积投影--地球面上的图形在投影后保持面积不变,称等面积投影。投影中变形椭圆为面积相等而形状不同的椭圆,这满足条件,面积比P=a×b=mnsinφ=1。
③任意投影--即不具备以上两种投影的,在任意投影中,如果沿某一主方向的长度比等于1,即a=1或b=1,则这种投影称为等距离投影。
2、根据正轴投影时经纬网形状的投影分类
①圆锥投影--投影中纬线为同心圆圆弧,经线为圆半径,且经线间的夹角与经差成正比例。该投影按变形性质可分为等角、等面积和任意(主要为等距离)圆锥投影。按球面坐标极点的位置,或按投影面与地球的相对位置不同可以分为正轴、横轴与斜轴圆锥投影,以及切(单标准纬线)和割(双标准纬线)圆锥投影,等角圆锥投影亦称为兰勃特正形圆锥投影,正轴等面积割圆锥投影也曾叫亚尔勃斯投影。
②圆柱投影--投影中纬线为一组平行直线,经线为垂直于纬线的另一组平行直线,且两相邻线之间的距离相等。等角圆柱投影亦叫墨卡托投影。等角横切椭圆柱投影即著名高斯—克吕格投影。等角横割椭圆柱投影也称通用横轴墨卡托投影。
③方位投影--投影中纬线为同心圆,经纬为圆的半径、且经线间的夹角等于地球面上相应的经差。等面积方位投影亦称为兰勃特等面积方位投影。等距离方位投影又称为波斯托投影。
④伪圆锥投影--投影中纬线为同心圆圆弧、经线为交于圆心的曲线,在一般情况下均对称于中央经线。等面积和任意伪圆锥投影主要是彭纳投影。
⑤伪圆柱投影--投影中纬线为一组平行直线,而经线为某种曲线,在一般情况下对称于中央经线。
⑥伪方位投影--投影中纬线为同心圆,而经线为交于圆心的曲线,在一般情况下投影中至少有一条直线,它是投影的对称轴。
⑦多圆锥投影--投影中纬线为同轴圆圆弧,其圆心在中央经线上,而经线为对称于中央经线的曲线。
下面将经纬线形状作一个小结:
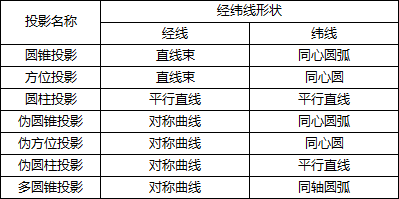
至此,我们介绍了投影按外部的经纬线形状和内在的变形特征的分类,对于一个投影,较完整的名称宜兼有两种分类,例如等角圆锥投影、等面积方位投影、等距离圆柱投影等。
3、地图投影变换
地图投影变换是研究从一种地图投影点的坐标变换为另一种地图投影点的坐标的理论和方法。在大地测量和地形测量中,往往需要进行不同坐标系间的坐标变换,即坐标换带计算。随着计算机地图制图的发展,研究地图投影变换的理论和方法日益重要和迫切,因为在采用制图自动作业中,必须首先提供从一种地图投影点的坐标变换为另一种地图投影点的坐标的关系式,即数学模式,才能进行这种作业,因为如果没有这两种不同投影点的坐标变换关系式,就无法编制出合乎变换要求的,适用于电子计算机进行变换所需要的程序设计,所以,地图投影变换已成为计算机地图制图的一个组成部分。
为了适应计算机地图制图、信息系统建设、遥测图象显示和定位,以及满足空间遥感技术和拓朴变换的需要,地图投影变换已逐步发展成为研究空间数据处理,以及空间点位和平面点变换的理论和方法及其应用的数学制图学的一个分支学科。地图投影变换可广义地理解为研究空间数据处理,变换及应用的理论和方法,它可表达为:
(x',y',z')---(φ,λ)---(x,y)---(X,Y)
地图投影变换可狭义地理解为建立两平面场之间点的一一对应的函数关系。
